专栏名称: 学霸数学
| 中考高考相关信息,数学学习的相关分享,学校教育/家庭教育/社会教育现象与案例分析 |
今天看啥
微信公众号rss订阅, 微信rss, 稳定的RSS源
目录
相关文章推荐

|
新北方 · “只要不穿校服就能买到”!不少中学生居然已经上瘾 · 6 小时前 |

|
新北方 · 车主请注意!近期发生多起,辽宁金融监管局发布 ... · 9 小时前 |

|
新北方 · 这种菜是天然“补钙剂”,钙含量不逊于牛奶,别错过! · 昨天 |

|
新北方 · 微信群里辱骂同学,6名中学生被诉至法院→ · 2 天前 |

|
新北方 · 明天温暖恍如初夏,4地最高温可达25℃! · 2 天前 |
推荐文章

|
新北方 · “只要不穿校服就能买到”!不少中学生居然已经上瘾 6 小时前 |

|
新北方 · 车主请注意!近期发生多起,辽宁金融监管局发布风险提示! 9 小时前 |

|
新北方 · 微信群里辱骂同学,6名中学生被诉至法院→ 2 天前 |

|
新北方 · 明天温暖恍如初夏,4地最高温可达25℃! 2 天前 |

|
巴伦中文 · 连跌四个月,但燃力士的增长故事还没讲完 6 月前 |
|
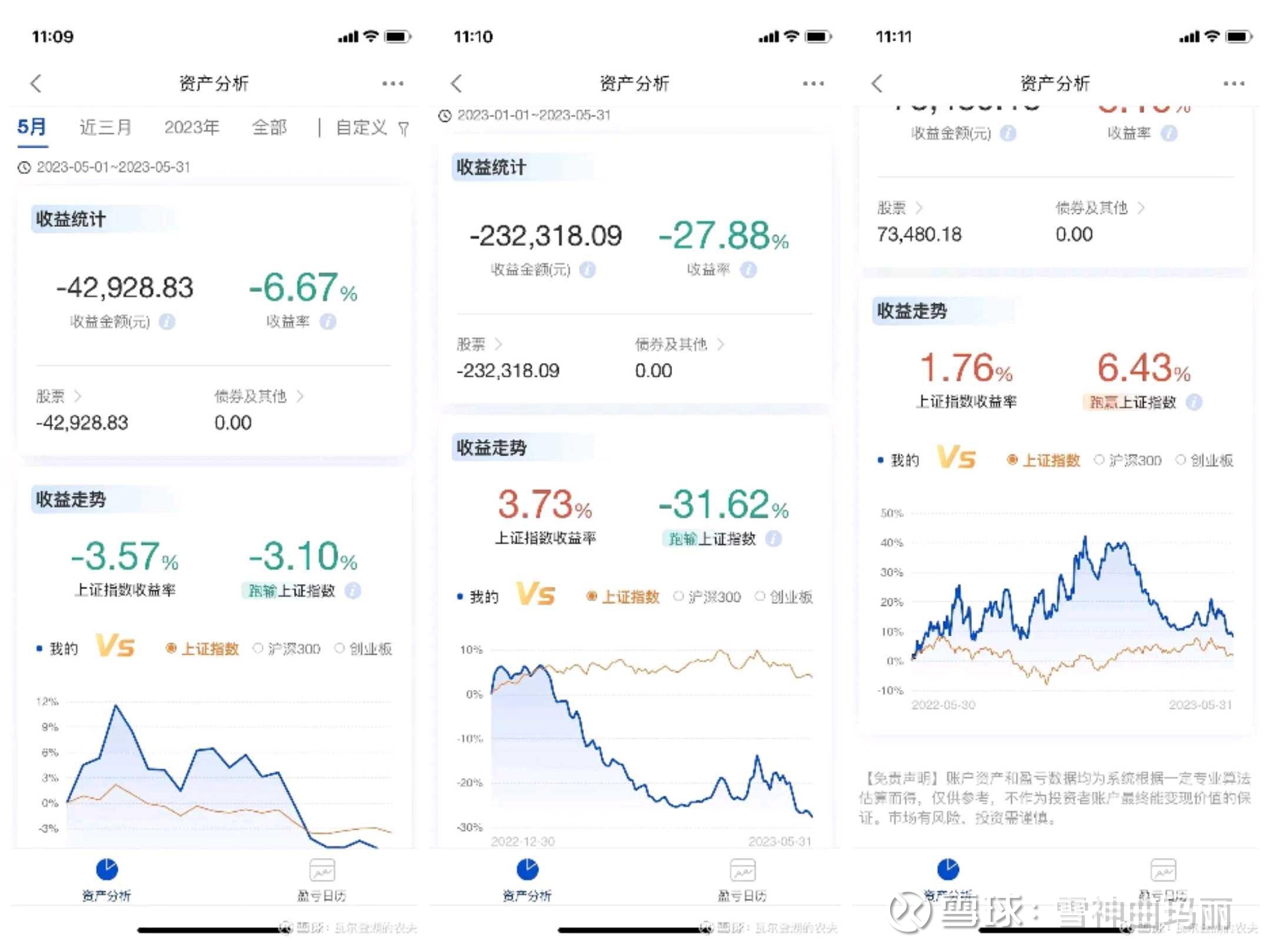
雪神曲玛丽 · -20241019094621 5 月前 |

|
鸡西新闻网 · 麻山区 | 热气腾腾备春耕 3 周前 |

|
JC万事通 · “网红地打卡”! 晋城人违法了! 1 周前 |

